LoginSignup
53
39

More than 5 years have passed since last update.

@inamiy(Yasuhiro Inami)

iOSDC Japan 2018 で発表した「圏論とSwiftへの応用」の補足

Last updated at Posted at 2018-09-05

この記事は、 iOSDC Japan 2018 で圏論について話しました ＋ Storyboard/AutoLayout相談会しました - Qiita の続編です。
先週、8月30日〜9月2日にかけて開催された iOSDC Japan 2018 で登壇発表した 「圏論とSwiftへの応用」 の補足になります。

CfP / スライド

発表の中では、 圏の定義 から始まり、 関手 、自然変換 の基本を押さえた後に、 米田の補題 、 随伴 、 モナド・コモナド について、疑似Swiftによる例を上げながら、一気に解説しました。

特に、関数型プログラミングを知っている人であれば、 継続 や カリー化 、 状態モナド 、 レンズ といった重要な単語が、いかに圏論と深く結びついているかが伺えると思います。

図式、コード例、バズワードの全マシマシな資料は、他にあまり見ないと思いますので、ぜひ圏論を一から勉強する際にお役立ていただければ幸いです。

疑似Swiftについて

スライドの中で使った疑似Swiftの記法ですが、例えば 「関手」 を次のように書きました：

// 疑似Swift
protocol Functor[F] {
    static func map<B>(_ f: A -> B) -> F<A> -> F<B>
}

extension Functor[Array] {  // NOTE: `extension Array: Functor` ではない！
    static func map<B>(_ f: A -> B) -> Array<A> -> Array<B> { ... }
}

ちなみに、関手を実現するには、いわゆる 高カインド多相 と呼ばれる言語機能が必要です。
が、残念ながら、Swift 4.2現在、まだ実装はされていません。
以前から、導入について沢山の意見・議論が交わされており、様々なシンタックスが提案されていますが、実装の見込みが薄いのが現状です。

今回、筆者が使った独自記法は、Haskellのtypeclassの形を参考にしています。

-- Haskell
class Functor f where
    fmap :: (a -> b) -> f a -> f b

また、それとなくScalaの記法にも似ていると思います。

// Scalaz
trait Functor[F[_]] extends InvariantFunctor[F] {
  def fmap[A, B](r: F[A], f: A => B): F[B]
}

typeclass の利点

Haskell風の typeclass の書き方を採用した背景として、 「複数」の型（コンストラクタ）の関係性を、インターフェースの定義の中に組み込める という利点があります。

例えば、スライドの中で 「随伴」 を以下のように定義しました：

protocol Adjunction[F, U] where Functor[F], Functor[U] {
    static func leftAdjunct<C, D>(_ f: F<C> -> D) -> C -> U<D>
    static func rightAdjunct<C, D>(_ f: C -> U<D>) -> F<C> -> D
}

extension Adjunction[Tuple<A>, Func<A>] { ... }
// NOTE: `Tuple<A>` は `Tuple<A, B> = Tuple<A><B>` とカリー化して、`A`だけ部分適用したもの

もし、これを通常のSwiftプロトコルを使って書こうとすると、少し厄介です：

protocol Adjunction: Functor {
    associatedtype U: Functor

    static func leftAdjunct<C, D>(_ f: Self<C> -> D) -> C -> U<D>
    static func rightAdjunct<C, D>(_ f: C -> U<D>) -> Self<C> -> D
}

extension Tuple<A>: Adjunction where Self.U == Func<A> { ... }

これは、 左随伴 F を起点 (Self) として、右随伴 U を assocatedtype に乗せて関係性を定義しています。

一方で、逆に考えると、このようにも書けます：

protocol Adjunction: Functor {
    associatedtype F: Functor

    static func leftAdjunct<C, D>(_ f: F<C> -> D) -> C -> Self<D>
    static func rightAdjunct<C, D>(_ f: C -> Self<D>) -> F<C> -> D
}

extension Func<A>: Adjunction where Self.F == Tuple<A> { ... }

今度は、 右随伴 U が起点 となっています。

つまり、 「単体」の型（コンストラクタ）を起点に、関係性を extension + where句で設定すると、インターフェースの定義方法が「複数可能」で、一意的な書き方ができない問題がある と言えます。
言い換えれば、 protocol + where によって、起点(Self)に依存しない関係性を、インターフェース定義段階で確定する ことができます。

ちなみに、Haskellにおける随伴の定義は、以下の通りです： Data.Functor.Adjunction

-- NOTE:
-- `Representable` は `Functor` 型クラスの継承
-- `| f -> u, u -> f` の意味は、 `f` or `u` が決まると、逆も自動的に決まる関係性 (functional dependency)
class (Functor f, Representable u) =>
      Adjunction f u | f -> u, u -> f where
  unit         :: a -> u (f a)
  counit       :: f (u a) -> a
  leftAdjunct  :: (f a -> b) -> a -> u b
  rightAdjunct :: (a -> u b) -> f a -> b

  unit           = leftAdjunct id
  counit         = rightAdjunct id
  leftAdjunct f  = fmap f . unit
  rightAdjunct f = counit . fmap f

ほぼ丸パクリ 疑似Swiftに比べて、よりシンプルな記法で書けることが分かります。

また、スライド中にあった、 「unit と counit」が、「leftAdjunct と rightAdjunct」から導ける ことが等式から分かりますし、逆もまた可能です。

ここで、等式中の . と id は、スライドの「圏の定義」で紹介した 「合成」と「恒等射」 です。
この2つの関数があることで、 unit/counit ↔ leftAdjunt/rightAdjunct が互いに変換可能です。
つまり、巡り巡って 「合成」と「恒等射」は圏における重要な構成要素 であると言えます。

米田の補題について


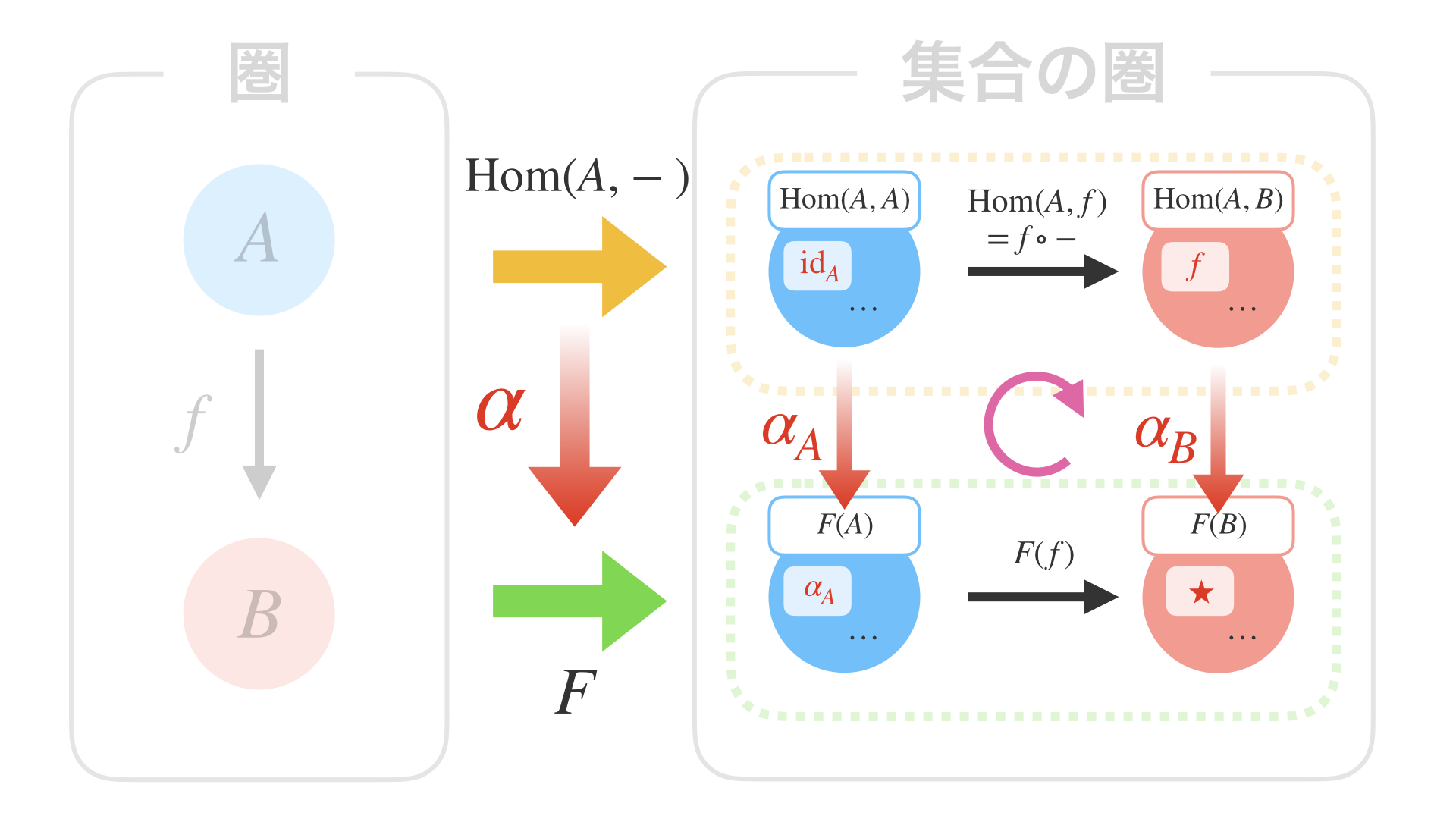
(https://speakerdeck.com/inamiy/iosdc-japan-1?slide=52 より)

当日の発表では、「米田の補題から先の話が分からなかった」という感想が多かったので、補足します。

圏論を学ぶ上で、最初の難関になるのが 「米田の補題」 です。
自然変換の始域（ドメイン）に Hom関手 (Hom-functor) と呼ばれる特殊な関手をおくことで導き出される補助定理です。

ここで、Hom関手の前にまず、 Hom集合 (Hom-set) について知っておく必要があります。
端的に言うと、Hom集合は、圏の対象 $A$ から $B$ に向かう 射の集合 のことで、$\mathrm{Hom}(A, B)$と書きます。
これは、型の圏で言うところの 「関数の型」 に相当します。要するに、 A -> B のことです。

Note:
A -> B と書くと、あたかも1本の射しか伸びていないように見えますが、この書き方は 図式とは異なる ので注意して下さい。
f: A -> B だったり g: A -> B だったり、「関数の 型の値 」は、通常、複数個が取り得ます。
「型」そのものが「集合」 だと思えば、 A -> B もまた 「関数の型」なので「射の集合」 になり、f や g は個々の射（射の集合の要素）になります。

この A -> B について、 ジェネリックな B （自然性） を考えたものを （共変）Hom関手 といいます。
一般に、 $\mathrm{Hom}(A, -)$ と書きますが、Swiftの型で例えるなら <B> A -> B や ∀B. A -> B 等と書けます。

これにより、先ほどの上の図式の右側にあった、「集合の圏」の対象 $\mathrm{Hom}(A, A)$ が、 $\mathrm{Hom}(A, -)$ に $A$ を適用 した結果であることが分かります。
型で書くと、 A -> A になります。

そして、ここが最も重要な点ですが、 A -> A の射の集合には必ず $\mathrm{id}_A$ が存在します。
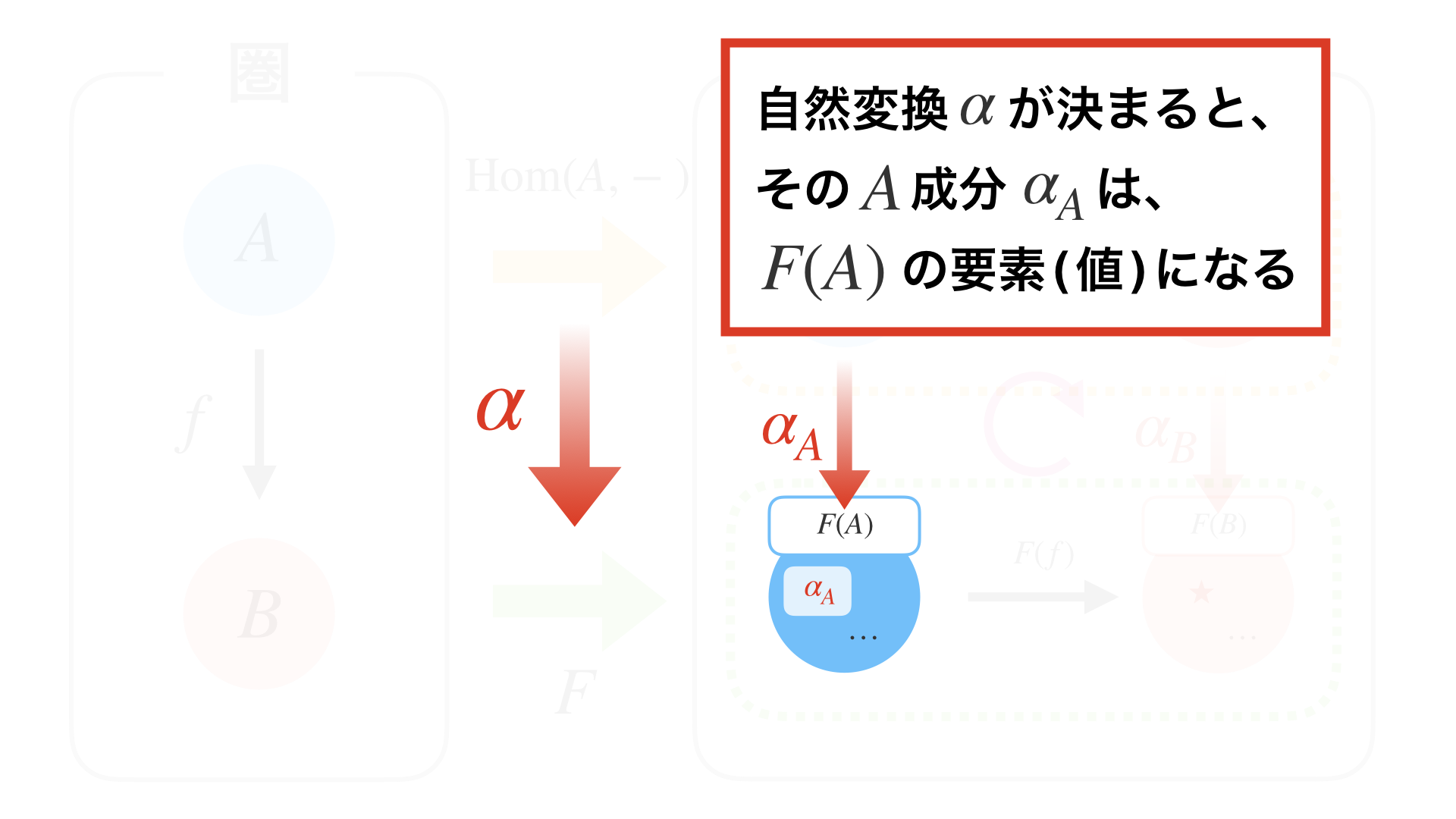
これに、自然変換（ジェネリック関数）

\alpha: \forall B. (A \to B) \to F(B)

を適用すると、$F(A)$ の値（要素） として $\alpha_A$ が得られ：

逆に、$\alpha_A$ が定まっている場合は、 可換図式 から、任意の $B$ について $\alpha_B$ が求まり、結果的に $\alpha$ そのものを導くことができます：

つまり、

\mathrm{Hom}(\mathrm{Hom}(A, -), F) \cong F(A) \\
\forall B. (A \to B) \to F(B) \cong F(A)

左辺の「ジェネリック関数の型」と、右辺の「値の型 $F(A)$ 」が 1:1 に対応します 。

おまけ： 米田の原理

米田の補題には双対バージョンがあり、 $F$ を 反変関手 とすれば、

\mathrm{Hom}(\mathrm{Hom}(-, A), F) \cong F(A) \\
\forall B. (B \to A) \to F(B) \cong F(A)

もまた成り立ちます。

ここで、 $F = \mathrm{Hom}(-, A')$ ないし $F(B) = B \to A'$ という反変関手を用いると、

\mathrm{Hom}(\mathrm{Hom}(-, A), \mathrm{Hom}(-, A')) \cong \mathrm{Hom}(A, A') \\
\forall B. (B \to A) \to (B \to A') \cong A \to A'

が得られますが、もし $A' \to A$ の逆変換もあるとすれば、 $A \cong A'$ になり、 $\mathrm{Hom}(-, A) \cong \mathrm{Hom}(-, A')$ を得ます。
これを 米田の原理 といいます。

つまり、 2つの 「値の型」 A と A' が同型かどうか を確認する際には、代わりに 2つの「ジェネリック関数の型」 B -> A と B -> A' が同型かどうか を確認すれば良い（実は計算が簡単）ということになります。

言い換えると、 値よりも（ジェネリック）関数で考える ことが圏論への第一歩であり、関数型プログラミングの醍醐味であるといえます。

・・・ということで、文章がだいぶ長くなってしまいました。
「圏論のオススメ勉強法」 については、また次回書こうと思います。

53
39
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
53
39